Question

Which equations represent hyperbolas?

Answer 1

Try this option:
1. Common view of hyperbola equation is:

`(x^2)/(a) - (y^2)/(b) =1 \ , where \ a,b-numbers`
2. hyperbolas are: 2x²+4x-5y²-10y+57=0 and -x²+12x+3y²+7y+11=0.

Answer 2

The correct options are 2 and 5.

Explanation:

The general form of conics is

`Ax^2+Bxy+Cy^2+Dx+Ey+F=0`

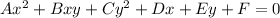
This equation represents the hyperbola if

`B^2-4AC>0`

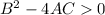
compare the given equations with the general equation.

In option 1,

`A=2,B=0,C=2,D=16,E=14,F=-9`

`B^2-4AC=(0)^2-4(2)(2)=-16<0`

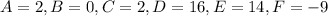
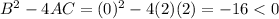
This equation does not represents a hyperbola.

In option 2,

`A=2,B=0,C=-5,D=4,E=-10,F=57`

`B^2-4AC=(0)^2-4(2)(-5)=40>0`

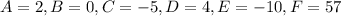
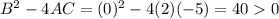
This equation represents a hyperbola.

In option 3,

`A=-1,B=0,C=-7,D=5,E=2,F=-81`

`B^2-4AC=(0)^2-4(-1)(-7)=-28<0`

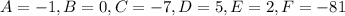
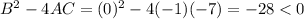
This equation does not represents a hyperbola.

In option 4,

`A=0,B=0,C=-2,D=1,E=4,F=15`

`B^2-4AC=(0)^2-4(0)(-2)=0`

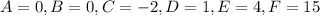
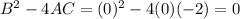
This equation does not represents a hyperbola.

In option 5,

`A=-1,B=0,C=3,D=12,E=7,F=11`

`B^2-4AC=(0)^2-4(-1)(3)=12>0`

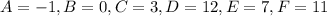
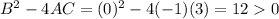
This equation represents a hyperbola.

Therefore the correct options are 2 and 5.