Answer:
Parent function is compressed by a factor of 3/4 and shifted to right by 3 units.
Explanation:
We are asked to describe the transformation of function
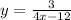 as compared to the graph of
as compared to the graph of
 .
.
We can write our transformed function as:
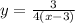

Now let us compare our transformed function with parent function.
Let us see rules of transformation.
 ,
,
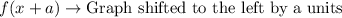 ,
,
Scaling of a function:
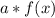
If a>1 , so function is stretched vertically.
If 0<a<1 , so function is compressed vertically.
As our parent function is multiplied by a scale factor of 3/4 and 3/4 is less than 1, so our parent function is compressed vertically by a factor of 3/4.
As 3 is being subtracted from x, so our parent function is shifted to right by 3 units or a horizontal shift to right by 3 units.
Therefore, our parent graph is compressed by a factor of 3/4 and shifted to right by 3 units to get our new graph.