Question

Can someone help me on this ? its Algebra 1 on exponents

Answer 1

The volume of a rectangular prism is its length times width times height, or algebraically,
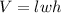
`V=lwh`. You may be used to computing volume with numbers, but remember, a variable is a stand-in for a number. So you can solve this in the same way. Substitute
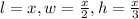
`l=x, w= (x)/(2),h= (x)/(3)` into the formula for volume. You get
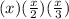
`(x)( (x)/(2))( (x)/(3) )`, and you multiply these factors together. As you would with ordinary fractions, multiply the numerators and denominators across. You get
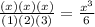
`((x)(x)(x))/((1)(2)(3)) = (x^3)/(6)`. It seems that the book wants you to simplify by bringing the 6 up to the denominator. Recall the rule
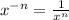
`x^(-n)= (1)/(x^n)`, if n is non-negative. The opposite applies so that
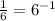
`(1)/(6) = 6^(-1)`. For your final answer, you write
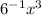
`6^(-1)x^3`. This corresponds to answer choice B.