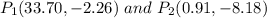We have a circumference that is given by the following equation:
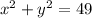
We can write this equation in its standard form as follows:

On the other hand, the linear function is given as the following table:
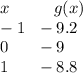
To check if the circle and the line intersects, let's substitute the equation of the line into the equation of the circle to see if there is a real solution, so:
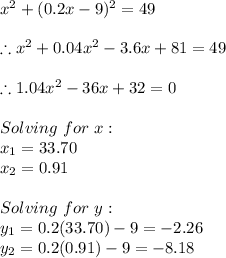
Finally the intersects are: