Binomial distribution can be used because the situation satisfies all the following conditions:1. Number of trials is known and remains constant (n=20)2. Each trial is Bernoulli (i.e. exactly two possible outcomes) (defective/normal)3. Probability is known and remains constant throughout the trials (0.05)4. All trials are random and independent of the othersThe number of successes(defects), x, is then given by
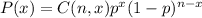
where
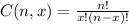
For n=20, p=0.05,
the mean number of defects is np=20*0.05=1
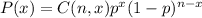
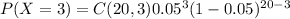
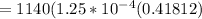
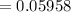
Answer: probability of exactly 3 defects in a sample of 20 is
0.05958