Question

A quality control engineer tests the quality of produced computers. suppose that 5% of computers have defects, and defects occur independently of each other.

a. what is the expected number of defective computers in a shipment of twenty? 1
b. find the probability of exactly 3 defective computers in a shipment of twenty.

Answer 1

Binomial distribution can be used because the situation satisfies all the following conditions:1. Number of trials is known and remains constant (n=20)2. Each trial is Bernoulli (i.e. exactly two possible outcomes) (defective/normal)3. Probability is known and remains constant throughout the trials (0.05)4. All trials are random and independent of the othersThe number of successes(defects), x, is then given by
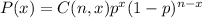
`P(x)=C(n,x)p^x(1-p)^(n-x)`where
`C(n,x)=(n!)/(x!(n-x)!)`
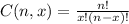
For n=20, p=0.05,
the mean number of defects is np=20*0.05=1


`P(x)=C(n,x)p^x(1-p)^(n-x)`

`P(X=3)=C(20,3)0.05^3(1-0.05)^(20-3)`

`=1140(1.25*10^(-4)(0.41812)`

`=0.05958`

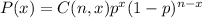
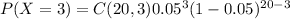
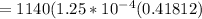
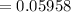
Answer: probability of exactly 3 defects in a sample of 20 is 0.05958