Answer:
∠B=157°
Explanation:
It is given that Quadrilateral ABCD is inscribed in the circle.
Also, we know that if the Quadrilateral ABCD is inscribed in the circle, then the opposite angles of the quadrilateral are supplementary by the property of circles. Then,
∠B+∠D=180°
⇒
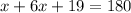
⇒
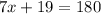
⇒
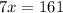
⇒
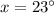
Thus, the value of ∠B=6x+19=6(23)+19=138+19=157°.