The average rate of change for any function f(x) is the ratio of change in its y-values to change in its x-values for any two particular points on the curve of the function f(x). Mathematically, we can write it as follows :-
Average rate of change =
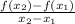
It says to find the average rate of change from x = 0 to x = 10.
From the given table, x = 0 corresponds to y = f(0) = -6 and x = 10 corresponds to y = f(10) = 204.
So we have two points A(0, -6) and B(10, 204).
Using the above formula, we can find average rate of change from A to B.
Average rate of change from (0, -6) to (10, 204) =
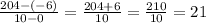
Hence, the final answer is 21.