Question

The table of values represents a quadratic function.

What is the average rate of change for f(x) from x = 0 to x = 10 ?

x ​f(x)​
​−10​ 184
​−5​ 39
0 ​−6​
5 49
10 204

Answer 1

The average rate of change for any function f(x) is the ratio of change in its y-values to change in its x-values for any two particular points on the curve of the function f(x). Mathematically, we can write it as follows :-

Average rate of change =
`(f(x_(2))-f(x_(1)))/(x_(2)-x_(1))`

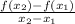
It says to find the average rate of change from x = 0 to x = 10.

From the given table, x = 0 corresponds to y = f(0) = -6 and x = 10 corresponds to y = f(10) = 204.

So we have two points A(0, -6) and B(10, 204).

Using the above formula, we can find average rate of change from A to B.

Average rate of change from (0, -6) to (10, 204) =
`(204-(-6))/(10-0) =(204+6)/(10) = (210)/(10) =21`

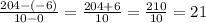
Hence, the final answer is 21.

Answer 2

(f(10) -f(0))/(10 -0) = (204 -(-6))/10 = 21

The average rate of change on the interval is 21.