Answer:
D). Y'=
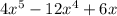 and y'=
and y'=
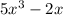
Explanation:
We are given the equation
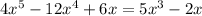 .
.
On simplifying this equation, we get
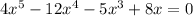
i.e. Let, Y'=
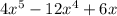 and y'=
and y'=
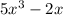
Now, according to the options,
A) Y =
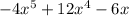 = -Y' , that means the graph will be inverse of the required graph.
= -Y' , that means the graph will be inverse of the required graph.
B) As the coefficient of 'x' in our given equation and the equation of option B are different, both will have different graphs.
C) As y =
 = -y', this means that the graph will be inverse of the required graph.
= -y', this means that the graph will be inverse of the required graph.
Hence, all above options are discarded and so option D is correct.