The correct option is: The range and domain of the graph are the same.
Explanation
Given function is:
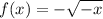
The inside term of a square root can't be negative, it will be always 0 or positive. That means,
 or
or

So, the Domain of the function is : "All real numbers such that
 "
"
Now, if x=0, then f(x) =0 and if x is any negative number, then f(x) will be also negative.
That means, the Range of the function: "All real numbers such that
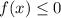 "
"
So, the range and domain of the function are the same.