Question

The length of a rectangle is twice its width. if the width is tripled and the length is decreased by 5, the area is increased by 4, find the width. D: help--

Answer 1

This one can besolved using system of equations. From the first statement we can assume that length = 2 * width. The area of rectange equals product of it's width and length. By knowing that and following to the second statement we get the second equation: (3 * width) * (length - 5) = width * length + 4. Let's mark the width as x and the length as y and write down our equations system:

`\begin{cases} y=2x \\ 3x\cdot (y-5)=xy+4 \end{cases}`

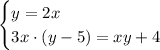
Using substituion method, lets replace every y with 2x within second equation and solve it:

`3x\cdot (2x-5)=x\cdot2x+4`

`6x^2-15x=2x^2+4`

`6x^2-15x-2x^2-4=0`

`4x^2-15x-4=0`

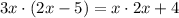
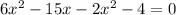
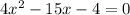
Now lets find the discriminant in order to solve this quadratic equation:

`D=b^2-4ac=15^2-4\cdot4\cdot(-4)=225+64=289`

`x_(1)=(-b+√(D))/(2a)=(15+√(289))/(2\cdot4)=(15+17)/(8)=(32)/(8)=4`

`x_(2)=(-b-√(D))/(2a)=(15-√(289))/(2\cdot4)=(15-17)/(8)=(-2)/(8)=-0.25`

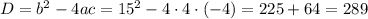
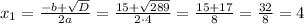
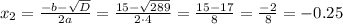
The second root is negative, so we ignore it as x represents width which can't be negative.
Now, using found root, let's find y value from the first equation:

`y=2x=2\cdot4=8`

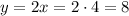
So, the width is equal 4 (and the length is equal 8).