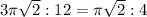A square is inscribed in a circle. If the area of the square is 9 in2, what is the ratio of the circumference of the circle to the perimeter of the square?

Question

asked Sep 13, 2019 6.5k views

2 Answers

Snovelli · Answer 1 · 2019-09-17T13:19:04+0000

The ratio of the circumference of the circle to the perimeter of the square is
$\pi √(2):4$

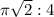
Step-by-step explanation

Area of the square = 9 inch²

If the side length of the square is
, then

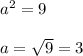
$a^2 = 9 \\ \\ a= √(9) =3$

So the side length of the square is 3 inch.

Now as the square is inscribed in a circle, so the diagonal of the square will be diameter of the circle.

Length of the diagonal of square =
a√(2) = 3√(2) inch

So, the diameter of the circle
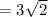= 3√(2) inch

If the radius of the circle is
, then

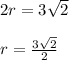
$2r = 3√(2) \\ \\ r= (3√(2))/(2)$

Circumference of the circle,
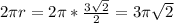$2\pi r= 2\pi *(3√(2))/(2)= 3\pi √(2)$ inch

and Perimeter of the square,
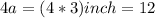4a = (4*3)inch= 12 inch

So, the ratio will be:
$3\pi √(2) : 12 = \pi √(2) : 4$