Answer: approximately 8.89 years
Step-by-step explanation: Let

Since the car loses 15% of the value after one year,
New value of car after one year = (previous value) - (15% of previous value)
New value of car after one year = (previous value) - 0.15 × (previous value)
New value of car after one year = 0.85 × (previous value) (1)
Based on our representation, if

represents the new value, then

represents the previous value. Using equation (1),

(2)
Moreover, note that
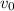
represents the initial value of the car. So, using equation (2),



.
.
.
So, doing this for n times, we have

(3)
In the problem, the initial value of the car is $28,000 and we need to find the value of n such that after n years the value of the car is $6,600.
So,

. Using equation (3),
