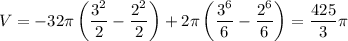Question

Let r r be the region enclosed by x=2 x = 2 , x=3 x = 3 , y=16-x^4 y = 16 − x 4 and y=0 y = 0 . find the volume of the solid obtained by rotating r r about y y -axis.

Answer 1

You have to use the "Cylinder Method" (aka "Shell Integration").
The volume of the solid obtained by rotating the region between f(x), y=0, x=a, and x=b is given by:


`V=\displaystyle\int^b_a f(x)\right \, dx`

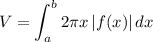
In your case,
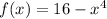
`f(x)=16-x^4`. So, substituiting f(x), a and b, and taking into account that in the interval (2,3) we can assume
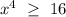
`x^4\ \ge \ 16`, and, therefore,
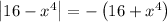
`\left|16-x^4\right| = -\left(16+x^4\right)`, we get:


`V=\displaystyle\int^3_2 2\pi x\left \, dx = \int^3_2 {-2\pi x\left(16-x^4\right)} \, dx = -2\pi\int^3_2 {\left(16x-x^5\right)} \, dx`

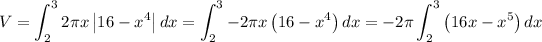
We have made use of the fact that you can take constant factors out of the integral.

Then, being the integral of the sum equal to the sum of the integrals:


`V = -2\pi\displaystyle\int^3_2 {\left(16x-x^5\right)} \, dx = -2\pi \int^3_2 {16x} \, dx + 2\pi \int^3_2 {x^5} \, dx`

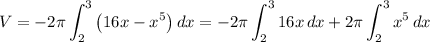
For both integrals we'll use the power integration rule, and the Second Fundamental Theorem of Calculus:


`\displaystyle \int {x^n} \, dx = (x^(n+1))/(n+1)`


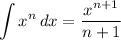
`V= -\displaystyle 2\pi \int^3_2 {16x} \, dx + 2\pi \int^3_2 {x^5} \, dx = -2\pi\cdot16\cdot\left[(x^2)/(2)\right]^3_2 + 2\pi\cdot\left[(x^6)/(6)\right]^3_2`

`V = -32\pi\left((3^2)/(2)-(2^2)/(2)\right) + 2\pi\left((3^6)/(6)-(2^6)/(6)\right) = (425)/(3)\pi`