Question

Find the x value for point C such that AC and BC form a 2:3 ratio. Segment AB is shown. A is at negative 3, 5. B is at 3, 0. 6 −0.6 4 −2.4

Answer 1

the answer is -0.6 hope this help

Answer 2

Hence, the x-value of point C is -0.6

Explanation:

The coordinates of A are (-3,5)

and the coordinates of B are (3,0).

Point C cuts the line segment AB in the ratio 2:3.

If any point C cut the line segment AB with vertices A(a,b) and B(c,d) in the ratio m:n, then the coordinates of point C(e,f) is given by:

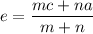`e=(mc+na)/(m+n)` and
`f=(md+nb)/(m+n)`

Here we have m=2 and n=3

a=-3,b=5 and c=3 and d=0.

Hence,
`e=(2*3+3*(-3))/(2+3)=(-3)/(5)=-0.6`

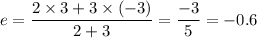
and
`f=(2*0+3*5)/(2+3)=(15)/(5)=3`

Hence the coordinates of point C is (-0.6,3).

Hence, the x-value of point C is -0.6.