Question

Find a solution of x dy dx = y2 − y that passes through the indicated points. (a) (0, 1) y = (b) (0, 0) y = (c) 1 6 , 1 6 y = (d) 4, 1 6 y =

Answer 1

The differential equation in question is x dy/dx = y^2 - y, which is a separable equation. The solution involves separating the variables, integrating both sides, and using the given initial conditions to find the particular solutions.

Step-by-step explanation:

The differential equation given is x dy/dx = y^2 - y, which can be rearranged to a separable form. To solve it, we separate variables and integrate:

First, we divide both sides by x(y^2 - y) to get:

dy/(y^2 - y) = dx/x

Now, we perform partial fraction decomposition on the left side:

1/(y(y-1)) = A/y + B/(y-1)

By finding A and B, we can then integrate both sides. After integration, we insert the initial conditions from each sub-question to find the particular solution that passes through the given points. Observe that while carrying out the integration, finding the constants for each case requires us to use the given initial conditions, which need to be treated case by case.

Without the actual integration, we cannot find the exact form of y as a function of x, but the steps provided guide us on how to approach this differential equation.

Answer 2

Answers:

(a)
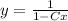
`y = (1)/(1 - Cx)`, for any constant C

(b) Solution does not exist

(c)
`y = (256)/(256 - 15x)`

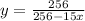
(d)
`y = (64)/(64 - 15x)`

Explanations:

(a) To solve the differential equation in the problem, we need to manipulate the equation such that the expression that involves y is on the left side of the equation and the expression that involves x is on the right side equation.

Note that


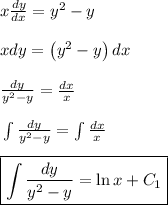
`x(dy)/(dx) = y^2 - y \\ \\ \indent xdy = \left ( y^2 - y \right )dx \\ \\ \indent (dy)/(y^2 - y) = (dx)/(x) \\ \\ \indent \int {(dy)/(y^2 - y)} = \int {(dx)/(x)} \\ \\ \indent \boxed{\int {(dy)/(y^2 - y)} = \ln x + C_1}` (1)

Now, we need to evaluate the indefinite integral on the left side of equation (1). Note that the denominator y² - y = y(y - 1). So, the denominator can be written as product of two polynomials. In this case, we can solve the indefinite integral using partial fractions.

Using partial fractions:


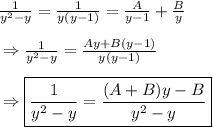
`(1)/(y^2 - y) = (1)/(y(y - 1)) = (A)/(y - 1) + (B)/(y) \\ \\ \indent \Rightarrow (1)/(y^2 - y) = (Ay + B(y-1))/(y(y - 1)) \\ \\ \indent \Rightarrow \boxed{(1)/(y^2 - y) = ((A+B)y - B)/(y^2 - y) }` (2)

Since equation (2) has the same denominator, the numerator has to be equal. So,


`image`

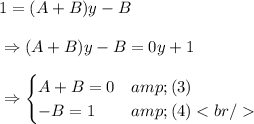
Based on equation (4), B = -1. By replacing this value to equation (3), we have

A + B = 0
A + (-1) = 0
A + (-1) + 1 = 0 + 1
A = 1

Hence,


`(1)/(y^2 - y) = (1)/(y - 1) - (1)/(y)`

So,


`\int {(dy)/(y^2 - y)} = \int {(dy)/(y - 1)} - \int {(dy)/(y)} \\ \\ \indent \indent \indent \indent = \ln (y-1) - \ln y \\ \\ \indent \boxed{\int {(dy)/(y^2 - y)} = \ln \left ( (y-1)/(y) \right ) + C_2}`

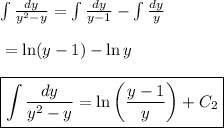
Now, equation (1) becomes


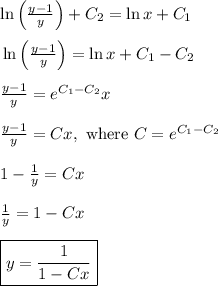
`\ln \left ( (y-1)/(y) \right ) + C_2 = \ln x + C_1 \\ \\ \indent \ln \left ( (y-1)/(y) \right ) = \ln x + C_1 - C_2 \\ \\ \indent (y-1)/(y) = e^(C_1 - C_2)x \\ \\ \indent (y-1)/(y) = Cx, \text{ where } C = e^(C_1 - C_2) \\ \\ \indent 1 - (1)/(y) = Cx \\ \\ \indent (1)/(y) = 1 - Cx \\ \\ \indent \boxed{y = (1)/(1 - Cx)}` (5)

At point (0, 1), x = 0, y = 1. Replacing these values in (5), we have


`y = (1)/(1 - Cx) \\ \\ \indent 1 = (1)/(1 - C(0)) = (1)/(1 - 0) = 1`

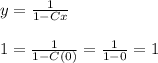
Hence, for any constant C, the following solution will pass thru (0, 1):


`\boxed{y = (1)/(1 - Cx)}`

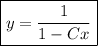
(b) Using equation (5) in problem (a),


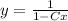
`y = (1)/(1 - Cx)` (6)

for any constant C.

Note that equation (6) is called the general solution. So, we just replace values of x and y in the equation and solve for constant C.

At point (0,0), x = 0, y =0. Then, we replace these values in equation (6) so that


`y = (1)/(1 - Cx) \\ \\ \indent 0 = (1)/(1 - C(0)) = (1)/(1 - 0) = 1`

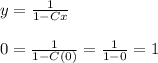
Note that 0 = 1 is false. Hence, for any constant C, the solution that passes thru (0,0) does not exist.

(c) We use equation (6) in problem (b) and because equation (6) is the general solution, we just need to plug in the value of x and y to the equation and solve for constant C.

At point (16, 16), x = 16, y = 16 and by replacing these values to the general solution, we have


`y = (1)/(1 - Cx) \\ \\ \indent 16 = (1)/(1 - C(16)) \\ \\ \indent 16 = (1)/(1 - 16C) \\ \\ \indent 16(1 - 16C) = 1 \\ \indent 16 - 256C = 1 \\ \indent - 256C = -15 \\ \indent \boxed{C = (15)/(256)}`

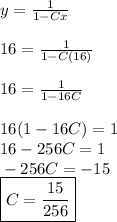
By replacing this value of C, the general solution becomes


`y = (1)/(1 - Cx) \\ \\ \indent y = (1)/(1 - (15)/(256)x) \\ \\ \indent y = (1)/((256 - 15x)/(256)) \\ \\ \\ \indent \boxed{y = (256)/(256 - 15x)}`

This solution passes thru (16,16).

(d) We do the following steps that we did in problem (c):
- Substitute the values of x and y to the general solution.
- Solve for constant C

At point (4, 16), x = 4, y = 16. First, we replace x and y using these values so that


`y = (1)/(1 - Cx) \\ \\ \indent 16 = (1)/(1 - C(4)) \\ \\ \indent 16 = (1)/(1 - 4C) \\ \\ \indent 16(1 - 4C) = 1 \\ \indent 16 - 64C = 1 \\ \indent - 64C = -15 \\ \indent \boxed{C = (15)/(64)}`

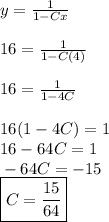
Now, we replace C using the derived value in the general solution. Then,


`y = (1)/(1 - Cx) \\ \\ \indent y = (1)/(1 - (15)/(64)x) \\ \\ \indent y = (1)/((64 - 15x)/(64)) \\ \\ \\ \indent \boxed{y = (64)/(64 - 15x)}`