Question

The variable x represents the number of long-sleeve shirts Nancy bought and the variable y represents the number of short-sleeve shirts she bought.

Nancy bought 531 shirts for her business. She bought 2 times as many short-sleeve shirts as long-sleeve shirts.

How many of each type of shirt did she buy?

Which system of equations models this problem?

{x−y=531
y=2x

{x+y=2
y=531x

{x+2y=531
y=2x

{x+y=531
y=2x

Answer 1

She bought 354 short-sleeve shirts and 177 long-sleeve shirts. The equation would be x+2y=531; y=2x

Answer 2

It is given that the variable x represents the number of long-sleeve shirts Nancy bought. The variable y represents the number of short-sleeve shirts she bought.

Also, it has been told that Nancy bought 531 shirts in total for her business.

Therefore, from the information presented in the above two paragraphs we know that
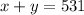`x+y=531`. This is because the number of half sleeve and full sleeve shirts add up to 531.

Thus, the first equation in the system is
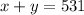`x+y=531`......(Equation 1)

Now, we also know that Nancy bought 2 times as many short-sleeve shirts as long-sleeve shirts. This can be mathematically represented by the equation:

`y=2x`

To find out how many of each type of shirt did Nancy buy we will have to find out the values of x and y.

Let us first find x. To do that we will simply substitute
`y=2x` in (Equation 1).

Thus,
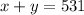`x+y=531` becomes
`x+2x=531`

`=3x=531`

`\therefore x=(531)/(3)=177`

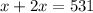
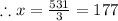
Thus, we can now find y as,
`y=2x=2* 177=354`

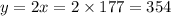
Therefore, the number of long sleeve shirts Nancy bought is 177 and the number of short sleeve shirts she bought is 354.

Also, the system of equations models this problem are:

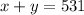`x+y=531` and
`y=2x` which is the last option in the given set of options.