Question

How can logarithms be graphed with different bases? How do transformations affect the logarithmic graph?

Answer 1

To graph with different bases, use the change of base formula.
Transformations may move the parent function.

Answer 2

1) Convert it to the same base and make a table with two columns for x, and y values.

2) The greater the base the lower the curve. Check the picture below.

Explanation:

1. Remember the rule in order to convert it to the same base two other logarithms:

`log_(a)b=(log_(c)a)/(log_(c) b)`

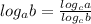
Example

`log_(5) 20 \\ log_(2) 4\\ \\(log_(10)20)/(log_(10)4) =(log2+log10)/(log2+log2) = 2,16`

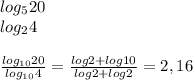
2. When we make the base bigger and bigger the curve will get closer and closer to the y-axis, such as those logarithmic functions.

Algebraically this is why

`y=log_(2)3=1.58`

`y=log_(10)3=0.477`

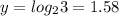
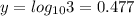
And so on...

3) Make a table for x values and plug the values to return the y values. Do not forget, x > 0

For
`y=log_(2)x`

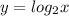
x y

1 0

2 1

4 2

`y=log_(10)x`

x y

1 0

2 0,3

4 0,6

Trace the hyperbole and check for yourself!