Answer:
1) Convert it to the same base and make a table with two columns for x, and y values.
2) The greater the base the lower the curve. Check the picture below.
Explanation:
1. Remember the rule in order to convert it to the same base two other logarithms:
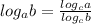
Example
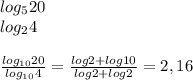
2. When we make the base bigger and bigger the curve will get closer and closer to the y-axis, such as those logarithmic functions.
Algebraically this is why
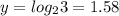
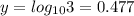
And so on...
3) Make a table for x values and plug the values to return the y values. Do not forget, x > 0
For
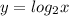
x y
1 0
2 1
4 2
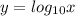
x y
1 0
2 0,3
4 0,6
Trace the hyperbole and check for yourself!