Question

If the range of f\left(x\right)=\sqrt{mx} and the range of g\left(x\right)=m\sqrt{x} are the same, which statement is true about the value of m?

Answer 1

`m` must be positive to have equal range between these functions.

Explanation:

The given functions are

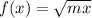`f(x)=√(mx)` and
`g(x)=m√(x)`

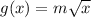
If we analyse each function, we'll notice that the range of
`f(x)` is all real numbers greater of equal than zero, because a square root can't give negative values.

The second funcion as the same range, all number greater or equal than zero, because it can't give a negative numbers, so they are ranges are the same.

However, their domains are

`D_(f):mx\geq 0\\D_(g): x\geq 0`

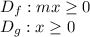
At this points, you may not notice the characteristic of
`m`, notice that the range of
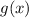`g(x)` has to have a restriction for
`m`, it must be greater or equal than zero, otherwise the ranges won't be the same.

Therfore,
`m` must be positive to have equal range between these functions.

Answer 2

So we are given two functions:

`f(x)=√(mx)\\g(x)=m\sqrt x`
The range of the function g is the following

`x\geq 0`.
The range of the function f is:

`m* x\geq 0`
Since the two ranges are equation, we deduce that the value of m is positive.
Otherwise the solution of the above inequality would be

`x\leq 0`
which is not the same as the first inequality.