Step-by-step explanation:
The vertical acceleration of the rocket is given by :
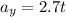
Acceleration is given by,
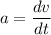

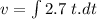
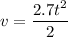 ..............(1)
..............(1)
Velocity is given by,
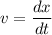
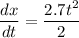


From above equation, we can find the value of t at x = 325 m
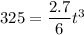
t = 8.97 s
Now put t = 8.97 s in equation (1) as :
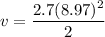
v = 108.62 m/s
So, the speed of the rocket when it is 325 meters above the surface of earth is 108.62 m/s. Hence, this is the required solution.