Question

A rocket starts from rest and moves upward from the surface of the earth. For the first 10.0 s of its motion, the vertical acceleration of the rocket is given by ay=(2.70m/s3)t, where the +y-direction is upward.What is the speed of the rocket when it is 325 m above the surface of the earth?

Answer 1

`a = 2.7t`

`v = \int\limits^t_0 {2.7t} \, dt = (2.7)/(2) t^2`

`x = \int\limits^t_0 {(2.7)/(2) t^2} \, dt = (2.7)/(6) t^3`

Solve for v with x = 325.

Answer 2

Step-by-step explanation:

The vertical acceleration of the rocket is given by :

`a_y=2.7t`

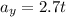
Acceleration is given by,
`a=(dv)/(dt)`

`(dv)/(dt)=2.7t`

`v=\int\limits{2.7\ t.dt}`

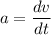
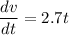
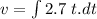
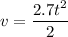`v=(2.7t^2)/(2)`..............(1)

Velocity is given by,
`v=(dx)/(dt)`

`(dx)/(dt)=(2.7t^2)/(2)`

`x=\int\limits{(2.7)/(2)t^2}.dt`

`x=(2.7)/(6)t^3`

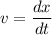
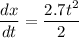
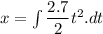
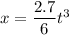
From above equation, we can find the value of t at x = 325 m

`325=(2.7)/(6)t^3`

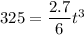
t = 8.97 s

Now put t = 8.97 s in equation (1) as :

`v=(2.7(8.97)^2)/(2)`

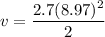
v = 108.62 m/s

So, the speed of the rocket when it is 325 meters above the surface of earth is 108.62 m/s. Hence, this is the required solution.