Answer:
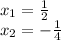
Explanation:
Hello
For ax2 + bx + c = 0,the values of x which are the solutions of the equation are given by
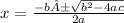
± means there are two solution for x, X1 and X2

Step 1
convert 8x2-2x=1 into the form ax2 + bx + c = 0 ( right side equal to cero)
subtract 1 in each side
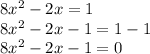
Step 2
replace in the equation
Let
a=8
b=-2
c=-1
Hence
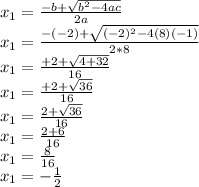
Now, X2
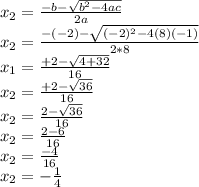
Have a great day