Question

The correct simplification of the quadratic formula used to solve 8x 2 - 2x = 1?

Answer 1

(2x−1)(4x+1)..................hope this helps

Answer 2

`x_(1)=(1)/(2)\\x_(2)=-(1)/(4)`

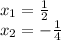
Explanation:

Hello

For ax2 + bx + c = 0,the values of x which are the solutions of the equation are given by

`x=\frac{-b±\sqrt{b^(2)-4ac } }{2a}`

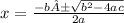
± means there are two solution for x, X1 and X2

`x_(1) =\frac{-b+\sqrt{b^(2)-4ac } }{2a} \\x_(2) =\frac{-b-\sqrt{b^(2)-4ac } }{2a}`

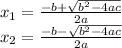
Step 1

convert 8x2-2x=1 into the form ax2 + bx + c = 0 ( right side equal to cero)

subtract 1 in each side

`8x^(2) -2x=1\\8x^(2) -2x-1=1-1\\8x^(2) -2x-1=0`

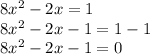
Step 2

replace in the equation

Let

a=8

b=-2

c=-1

Hence

`x_(1) =\frac{-b+\sqrt{b^(2)-4ac }}{2a}\\ x_(1)=\frac{-(-2)+\sqrt{(-2)^(2)-4(8)(-1) } }{2*8}\\x_(1) =(+2+√(4+32 ))/(16)\\x_(1) =(+2+√(36 ) )/(16)\\x_(1) =(2+√(36 ))/(16)\\x_(1) =(2+6)/(16) \\x_(1) =(8)/(16) \\x_(1)=-(1)/(2)`

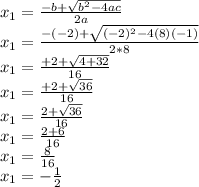
Now, X2

`x_(2) =\frac{-b-\sqrt{b^(2)-4ac }}{2a}\\ x_(2)=\frac{-(-2)-\sqrt{(-2)^(2)-4(8)(-1) } }{2*8}\\x_(1) =(+2-√(4+32 ))/(16)\\x_(2) =(+2-√(36 ) )/(16)\\x_(2) =(2-√(36 ))/(16)\\x_(2) =(2-6)/(16) \\x_(2) =(-4)/(16) \\x_(2)=-(1)/(4)`

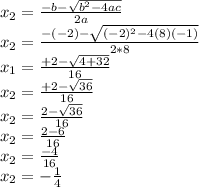
Have a great day