Answer:
58 months
Explanation:
This is a problem about compound interest, which formula is:
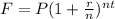
 : Future value. ($200,000)
: Future value. ($200,000)
 : Present value. ($3,000)
: Present value. ($3,000)
 : Annual percentage rate (APR) changed into a decimal. (7%)
: Annual percentage rate (APR) changed into a decimal. (7%)
 : Numbers of years. (?)
: Numbers of years. (?)
 : Number of compounding periods per year (12)
: Number of compounding periods per year (12)
Replacing all given values into the formula, we have:
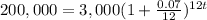
Therefore, approximately 58 months to grow the account to $200,000.