Question

You are considering investing in a bank account that pays a nominal annual rate of 7%, compounded monthly. If you invest $3,000 at the end of each month, how many months will it take for your account to grow to $200,000?

Answer 1

It would take around 67 monthes

Answer 2

58 months

Explanation:

This is a problem about compound interest, which formula is:

`F=P(1+(r)/(n))^(nt)`

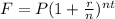
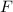`F`: Future value. ($200,000)

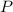`P`: Present value. ($3,000)

`r`: Annual percentage rate (APR) changed into a decimal. (7%)

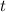`t`: Numbers of years. (?)

`n`: Number of compounding periods per year (12)

Replacing all given values into the formula, we have:

`200,000=3,000(1+(0.07)/(12))^(12t)`

`200,000=3,000(1+(0.07)/(12))^(12t)\\(200,000)/(3,000)=(1.006)^(12t)\\66.67=(1.006)^(12t)\\ln66.67=ln((1.006)^(12t))\\ln66.67=12t(ln(1.006))\\t=(ln66.67)/(12(ln(1.006)))\\t \approx 58.5`

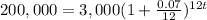
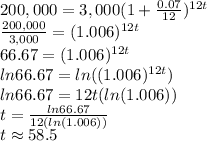
Therefore, approximately 58 months to grow the account to $200,000.