The half-life of a first order reaction is in how much τtime, the concentration of the reactant halves. After one half-life, the concentration of the reactant becomes half its initial value. After another half-life, itsconcentration becomes (M: initial concentration):
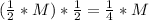
In general, after n half-lifes, the concentration of the reactant becomes:

Since 1/16=
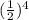
, we have that 4 half-lifes need to pass so that the concentration of the reactant becomes 1/16 of the initial one (=1/16*M). Hence, 4*22.9 sec=91.6 seconds is the required time.