Answer:
Area under the curve
f(x)=x², from x=1 to x=5 will be equal to
![=\int\limits^5_1 {x^2} \, dx \\\\=[(x^3)/(3)]\left \{ {{x=5} \atop {x=1}} \right.\\\\=(5^3)/(3)-(1^3)/(3)\\\\ =(125)/(3)-(1)/(3)\\\\=(124)/(3)](https://img.qammunity.org/2019/formulas/mathematics/high-school/7957gsxbs5hmjwxuugw7jx25vaupz2wjr0.png)
Area of the curve to the nearest integer=41 square units
⇒Using Rectangles Only
Area of Rectangle=Length × Breadth
→x=1, gives, y=1
→x=2, gives, y=4
Area of First rectangle =1×4=4 Square unit
→x=3, gives, y=9
Area of Second rectangle =1×9=9 Square unit
→x=4, gives, y=16
→x=5, gives, y=25
Area of Third rectangle =1×16=16 Square unit
Area of fourth rectangle =1×25=25 Square unit
Area of Rectangles=4+9+16+25
=54 square units
Area of Triangle
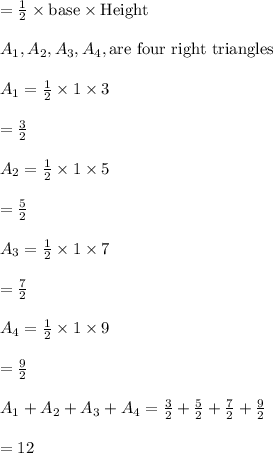
Required Area of the Region
= Area of four Rectangles -Area of Triangle
=54 Square unit - 12 Square unit
=42 Square Unit