Question

Estimate the area under the curve f(x) = x2 from x = 1 to x = 5 by using four inscribed (under the curve) rectangles. Answer to the nearest integer.

Answer 1

check the picture below.

Answer 2

Area under the curve

f(x)=x², from x=1 to x=5 will be equal to

`=\int\limits^5_1 {x^2} \, dx \\\\=[(x^3)/(3)]\left \{ {{x=5} \atop {x=1}} \right.\\\\=(5^3)/(3)-(1^3)/(3)\\\\ =(125)/(3)-(1)/(3)\\\\=(124)/(3)`

Area of the curve to the nearest integer=41 square units

⇒Using Rectangles Only

Area of Rectangle=Length × Breadth

→x=1, gives, y=1

→x=2, gives, y=4

Area of First rectangle =1×4=4 Square unit

→x=3, gives, y=9

Area of Second rectangle =1×9=9 Square unit

→x=4, gives, y=16

→x=5, gives, y=25

Area of Third rectangle =1×16=16 Square unit

Area of fourth rectangle =1×25=25 Square unit

Area of Rectangles=4+9+16+25

=54 square units

Area of Triangle

`=(1)/(2) * \text{base} * \text{Height}\\\\A_(1),A_(2),A_(3),A_(4),\text{are four right triangles}\\\\A_(1)=(1)/(2) *1 * 3\\\\=(3)/(2)\\\\A_(2)=(1)/(2) * 1 * 5\\\\=(5)/(2)\\\\A_(3)=(1)/(2) * 1 * 7\\\\=(7)/(2)\\\\A_(4)=(1)/(2) * 1 * 9\\\\=(9)/(2)\\\\A_(1)+A_(2)+A_(3)+A_(4)=(3)/(2)+(5)/(2)+(7)/(2)+(9)/(2)\\\\=12`

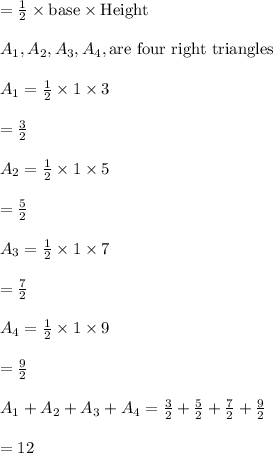
Required Area of the Region

= Area of four Rectangles -Area of Triangle

=54 Square unit - 12 Square unit

=42 Square Unit