Answer:
Option B is correct
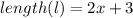 ;
;
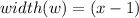
Explanation:
Given an area of rectangle in the form of equation:
Area of Rectangle =
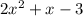
Formula for the Area of Rectangle: To find the Area of Rectangle in square unit, we multiply the length by width, i.e,
Area of Rectangle (A) =
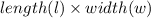
Factorize the quadratic equation:
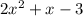
⇒
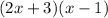
Since, Area of rectangle =
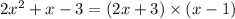
or
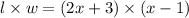
then, either
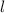 = (2x+3) ,
= (2x+3) ,
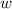 = (x-1) or
= (x-1) or
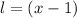 ,
,
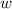 = (2x+3)
= (2x+3)
The only options we have;
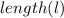 = (2x+3) and width (w) = (x-1)
= (2x+3) and width (w) = (x-1)