Answer:
Labelled the diagram as shown below
Given triangle ABC and triangle CDE are similar.
by definition of similar triangle:
Corresponding sides are in proportion:
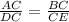
Here, AC = 8 units, DC =8+6 = 14 units, and BC = 2x-2 units and CE= 3x units.
Substitute these we have;
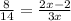
Simplify:

By cross multiply we have;
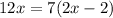
Using distributive property:
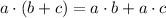
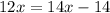
Subtract 14x from both sides we get;
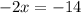
Divide by b-2 to both sides we get;
x = 7
Therefore, the value of x is, 7