Question

The two triangles are similar.

What is the value of x?



Enter your answer in the box.

Answer 1

Find the scale factor then multiply the side that is the same way as X then you got your answer mate if you don't understand it I'm open to direct message.

Answer 2

Labelled the diagram as shown below

Given triangle ABC and triangle CDE are similar.

by definition of similar triangle:

Corresponding sides are in proportion:

`(AC)/(DC) =(BC)/(CE)`

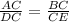
Here, AC = 8 units, DC =8+6 = 14 units, and BC = 2x-2 units and CE= 3x units.

Substitute these we have;

`(8)/(14) =(2x-2)/(3x)`

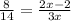
Simplify:

`(4)/(7) =(2x-2)/(3x)`

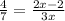
By cross multiply we have;

`12x = 7(2x-2)`

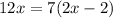
Using distributive property:
`a\cdot (b+c) = a\cdot b+ a\cdot c`

`12x = 14x-14`

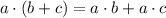
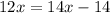
Subtract 14x from both sides we get;

`-2x = -14`

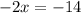
Divide by b-2 to both sides we get;

x = 7

Therefore, the value of x is, 7