Answer:
The events, rolling a sum of 6 and rolling doubles are not independent events
Explanation:
We know that two events A and B are independent if:

where P denotes the probability of an event.
Let A denote the event of rolling a sum of 6
and B denote the event of rolling a double.
Then A∩B denote the event of rolling a double whose sum is 6.
Now we know that there are a total of 36 outcomes on rolling two die
Now
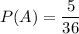
( Since there are 5 outcomes such that sum of the roll is: 6
i.e. (1,5), (2,4) , (3,3) , (4,2) and (5,1) )
Also,
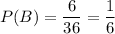
( Since there are a total of 6 events which are double
i.e. (1,1) (2,2) (3,3) (4,4) (5,5) and (6,6) )
This means that:
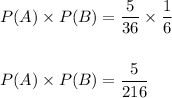
Also, A∩B is the outcome (3,3)
Hence, we have:
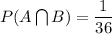
Hence, we get:

Hence, the events are not independent.