Answer:
Using distance(D) formula for two points is given by:
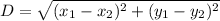
From the given figure:
The coordinates of the quadrilateral ABCD are:
A(-3, 2), B(4, 2), C(3, -3) and D(-3, -3)
For A(-3, 2) and B(4, 2)
using formula we have;

⇒
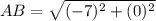
⇒
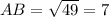 units
units
Similarly;
For B(4, 2) and C(3, -3)
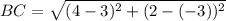
⇒
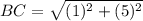
⇒
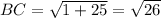 units.
units.
For C(3, -3) and D(-3, -3)

⇒
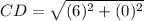
⇒
 units.
units.
For A(-3, 2) and D(-3, -3)
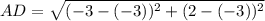
⇒
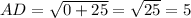 units.
units.
Perimeter is equal to the sum of all the sides of quadrilateral ABCD:
Perimeter = AB+BC+CD+AD
then;
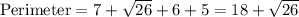 units
units
Therefore, the perimeter of quadrilateral ABCD is,
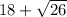 units
units