ANSWER
The value of x for which
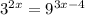
is
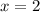
Step-by-step explanation
The given equation is
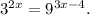
This is an indicial equation or an exponential equation in x.
We can see that, this time, the variable is in the numerator.
So we need to express both sides of the equation to the same base to obtain,
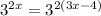
Since the base are the same, we can now equate the exponents to get,
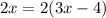
When we divide both sides of the equation by 2, we obtain,
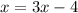
We now group like terms to obtain,
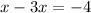
We simplify the left hand side to get,
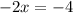
We finally divide through by negative 2 to obtain,
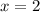
Therefore the correct answer is B.