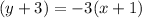Help asap, please! Thanks!

Question

asked Jul 11, 2019 161k views

2 Answers

Poloniki · Answer 1 · 2019-07-16T14:23:14+0000

Solution:

As we know that the equation of a straight line passing through a given point and having slope m is given by

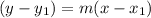
(y-y_1)=m(x-x_1)

Here we can find the slope of the line from the given points (-3,3) and (-1,-3)

Slope of the line can be found using the formula

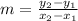
$m=(y_2-y_1)/(x_2-x_1)\\$

Here the points are (-3,3) and (-1,-3) So the slope will be

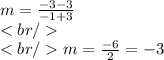
Hence the equation of the straight line will be

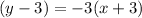
(y-3)=-3(x+3)

or

(y+3)=-3(x+1)