Question

For an absolute value equation, there are two solutions. Use the given equation and it’s solutions to algebraically prove this statement to be true |x|=9 (show work so I understand how to do it as well please!!)

Answer 1

The first sentence is not true in general. Consider the equation
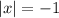
`|x|=-1`. There are no solutions. Now consider
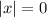
`|x|=0`. There is only one solution,
`x=0`.

But whatever. You're asked to demonstrate that
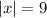
`|x|=9` has two solutions (which is true; the right hand side must be a positive integer in order to have two solutions). This follows immediately from the definition of absolute value, which says


`|x|=\begin{cases}x&\text{for }x\ge0\\-x&\text{for }x<0\end{cases}`

So suppose
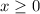
`x\ge0`. Then


`|x|=9\implies x=9`

Now suppose
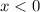
`x<0`. Then


`|x|=9\implies -x=9\implies x=-9`

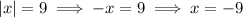
So two solutions to
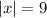
`|x|=9` are
`x=\pm9`.

Answer 2

x = 9 or -9
this is true because absolute value means the distance from 0 and on a number line it takes 9 jumps to get from 9 and -9.