Question

Given f(x)=2x2−3 and g(x)=x+4 . What is (fg)(x) ?

A)2x3−12
B)2x2+x+1
C) 2x3+8x2−3x−12
D) −2x2+x+7

Answer 1

`(fg)(x)=f(x)g(x)=(2x^2−3)(x+4)=2x^3+8x^2-3x-12`

or

(fg)(x)=f(x)g(x)=(2x^2−3)(x+4)=2x^3+8x^2-3x-12

Answer 2

Option (c) is correct

`(fg)(x)=2x^3+8x^2-3x-12`

Step-by-step explanation:

Given : functions
`f(x)=2x^2-3` and
`g(x)=x+4`

We have to calculate (fg)(x) and choose the correct from the given options.

Consider (fg)(x) = (f • g)(x) = f(x) • g(x)

That is we have to multiply the two functions.

Consider the given functions
`f(x)=2x^2-3` and
`g(x)=x+4`

Then,

`f(x)\cdot g(x) =(2x^2-3)(x+4)`

Multiply the each term of first bracket with each term of second bracket, we have,

`f(x)\cdot g(x) =2x^2\cdot (x+4)-3\cdot(x+4)`

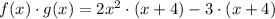
Simplify, we have,

`f(x)\cdot g(x) =2x^3+8x^2-3x-12`

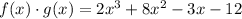
Thus,
`(fg)(x)=2x^3+8x^2-3x-12`

Option (c) is correct.