Question

The function V(t) = 2.99(1.12) represents the value V(t), in dollars, of a commemorative box of Wheaties t years after its purchase in 2000. Determine the annual growth rate in the value of the Wheaties box. How much is the box worth currently in the year 2021)? Round to the nearest cent (2 decimal places)

Answer 1

Answer: The annual growth rate in the value of the Wheaties box = 12%

The box worth $32.30 currently in the year 2021.

Explanation:

Exponential growth function :
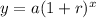`y=a(1+r)^x` , where a = initial value, r= rate of growth , x= time (i)

Given:
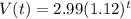`V(t) = 2.99(1.12)^t` , where V(t) = value of a commemorative box of Wheaties t years after its purchase in 2000.

It can written as

`V(t) =2.99(1+0.12)^t`

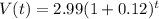
Comparing above function with (i), we get r=0.12

The annual growth rate in the value of the Wheaties box = 12%

Now , For 2021 , t=2021-2000=21

`V(21)=2.99(1.12)^(21)\approx32.30`

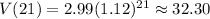
Hence, the box worth $32.30 currently in the year 2021.