Answer: The annual growth rate in the value of the Wheaties box = 12%
The box worth $32.30 currently in the year 2021.
Explanation:
Exponential growth function :
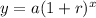 , where a = initial value, r= rate of growth , x= time (i)
, where a = initial value, r= rate of growth , x= time (i)
Given:
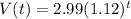 , where V(t) = value of a commemorative box of Wheaties t years after its purchase in 2000.
, where V(t) = value of a commemorative box of Wheaties t years after its purchase in 2000.
It can written as
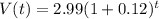
Comparing above function with (i), we get r=0.12
The annual growth rate in the value of the Wheaties box = 12%
Now , For 2021 , t=2021-2000=21
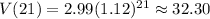
Hence, the box worth $32.30 currently in the year 2021.