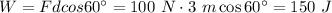Question

A sailboat moves north for a distance of 15.00 km when blown by a wind from the exact southeast with a force of 3.00 x 10^-4 N. The sailboat travels the distance in 1.0 h. How much work was done by the wind? What was the winds power? Must show all work A sailor pushes a 195.0 kg crate up a ramp that is 2.00 m high and 6.00 m long onto the deck of a ship. He exerts a 750.0 N force parallel to the ramp. What is the mechanical advantage of the ramp? what is the efficiency of the ramp? Must show all work A man lifts various loads with the same lever. The distance of the applied force from the fulcrum is 2.50 m and the distance from the fulcrum to the load is 0.500 m. A graph of resistance force vs. effort force s shown. What is the mechanical advantage of the lever? What is the ideal mechanical advantage of the lever? what is the efficiency of the lever? Show all work A girl places a stick at an angle of 60.0 degrees against a flat rock on a frozen pond. She pushes at an angle and moves the rock horizontally for 3.00 m across the pond at a velocity of 5.00 m/s and a power of 250.0 W. What force did she apply to the stick? How much work did she do? Show all work

Answer 1

The problems provided cover topics such as work, power, mechanical advantage, and efficiency within the framework of physics, using principles and formulas to calculate the required quantities for each scenario.

Step-by-step explanation:

The student has presented various problems that all relate to the concepts of work, power, mechanical advantage, and efficiency in physics. Each problem requires the use of different physics formulas to solve for the quantities of interest.

For example, for the sailboat problem, the work done by the wind can be calculated using the work-energy principle which states that work done is equal to the change in kinetic energy. Since the boat moves north and the wind blows from the southeast, the wind does no work because the force is perpendicular to the displacement. For the power of the wind, it's the work done per unit time, which in this case is 0 W since no work is done.

The mechanical advantage of the ramp is the ratio of the load force to the effort force. The efficiency is calculated as the ratio of the work output to the work input, expressed as a percentage. For the lever problem, the mechanical advantage is the ratio of the effort arm length to the resistance arm length. The ideal mechanical advantage is the same as the actual mechanical advantage if there is no friction. Efficiency is the ratio of actual mechanical advantage to the ideal mechanical advantage times 100%.

For the girl pushing the stick problem, the force applied can be found using the power formula which relates power to force times velocity, and work done can be calculated as the product of the force applied and the distance moved in the direction of the force.

Answer 2

These are actually 4 different exercises:

ex 1) The sailboat moves north, while the wind moves from southeast. This means the angle between the direction of the boat and the wind is
`45^(\circ)`.

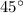
Calling F the force of the wind, and
`d=15~km=15000~m` the distance covered by the boat, the work done by the wind is:

`W=Fdcos{\theta}=3\cdot10^(-4)~N \cdot 15000~m\cdot cos 45^(\circ)=3.18~J`

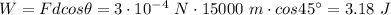
The total time of the motion is
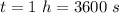
`t=1~h=3600~s` and therefore the power of the wind is

`P= (W)/(t) = (3.18~J)/(3600~s)=8.8\cdot10^(-4)~W`

ex 2) First of all, let's calculate the length of the ramp. Given the two sizes 2.00 m and 6.00 m, we have

`d= √((2~m)^2+(6~m)^2)= 6.32~m`

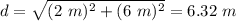
The mechanical advantage (MA) of the ramp is the ratio between the output load (W) and the input force (F). The output load is the weight of the load, mg, therefore:

`MA= (W)/(F)= (mg)/(F)= (195~Kg\cdot 9.81~m/s^2)/(750~N)=2.55`

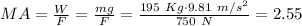
Finally, the efficiency
`\epsilon` of the ramp is the ratio between the output energy and the work done. The output energy is simply the potential energy (Ep) of the load, which is mgh, where h is the height of the ramp. The work done W is the product between the input force, F, and the displacement of the load, which is the length of the ramp: Fd. Therefore:

`\epsilon = (E_p)/(W)= (mgh)/(Fd)= (195~Kg \cdot 9.81~m/s^2\cdot 2~m)/(750~N\cdot6.32~m)=0.81`

ex 3) the graph is missing

ex 4) We know that the power is the ratio between the work done W and the time t:

`P= (W)/(t)`
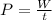
But we can rewrite the work as

`W=Fdcos\theta`
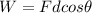
where F is the force applied, d the displacement of rock and
`\theta=60^{\circ]` is the angle between the direction of the force and the displacement (3 m).
Therefore we can rewrite the power as

`P= (W)/(t) = (F d cos\theta)/(t)=F v cos\theta`
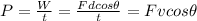
where
`v=d/t=5~m/s` is the velocity, Using the data of the exercise, we can then find the force, F:

`F= (P)/(v cos\theta) = (250~W)/(5~m/s \cdot cos 60^(\circ))=100~N`

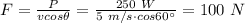
and now we can also calculate the work, which is

`W=Fdcos 60^(\circ)=100~N\cdot 3~m \cos60^(\circ)=150~J`