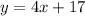Question

Help please.

Harrison pours sand into a bucket at a constant rate


A.y=3x+19

B.y=4x+17

C.y=4x-17

D.y=2x+21

Answer 1

The equation of the line parallel to the line on the graph that passes through (2,25) is

B.
`y=4x+17`

Explanation:

1. First find the equation of the line.

The equation of the line is represented by the equation
`y=mx+b`, where m is the slope and b is the intercept with y axis.

Find the slope in order tu find the equation of the line.

The slope is given by the equation
`m=(y_(2)-y_(1))/(x_(2)-x_(1))` where the points
`y_(2)`,
`y_(1)`,
`x_(2)` and
`x_(1)` are a pair of data from the graph.

The problem says that after 10 seconds the total weight is 50 ounces, so this is the first pair of data (10,50) and the second pair is the incercept with y axis (0,10), so the slope can be calculated as:

`m=(50-10)/(10-0)`

`m=4`

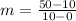
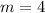
Finally b is the value of the intercept of the line with y axis, that is 10.

Therefore the line equation will be
`y=4x+10`

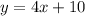
2. Find the equation of the parallel line:

The parallel line must be the same slope that is
`m=4`

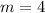
And as the parallel line to the line on the graph passes through (2,25) it means that the values of x and y for the parallel line are:

x=2

y=25

So,

`y-25=4(x-2)`

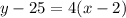
Solving for y:

`y=4x-8+25`

`y=4x+17`

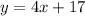
Therefore the equation of the line parallel to the line on the graph that passes through (2,25) is
`y=4x+17`

Answer 2

we can find the equation of line when given two points or a point and the gradient/slope.
In the above line we have two points (0,10) and (10,50),
The slope of the line is therefore 4
Parallel lines have equal slopes or gradient, therefore the slope of the other line is still 4. And the line pases through a point (2,25), hence
Equation will be, (y-25)/(x-2) = 4
= y-25 = 4x-8
= y =4x +17
Thus the appropriate equation is y = 4x +17