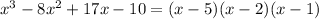Answer:
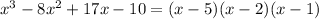
Explanation:
Given : Equation -
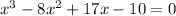
To Find : All real solutions of the equation
Step1 - Write the equation :
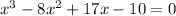
Step 2 : To find the x-intercept we plot the graph,
when we plot the graph the points where y=0 are the x-intercept
Step 3: Points where y=0 are 5,2,1 (shown in the attached graph)
Therefore, (x-5)(x-2)(x-1) are the solutions of the equation.
Hence,