Question

Compare and Contrast: Below are two expressions. Simplify each and choose the statement that is true about each. Expression #1 Expression #2 (4x)2(x) (6x2)4 The exponents in Expression #1 are greater than the exponents of Expression #2. The exponents on Expression #2 are greater than the exponents of Expression #1. The exponents of Expression #1 are the same as the exponents of Expression #2. The relationship cannot be determined with the given information.

Answer 1

its gonna be B. Look at the exponents and see witch end up bigger. its how i found it out,
tell me if im wrong
r u in FLVS

Answer 2

The exponents on Expression #2 are greater than the exponents of Expression #1

Explanation:

We have the expression as
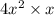`4x^(2)* x` and
`(6x^(2))^(4)`

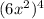
On simplifying the given expressions, we get,

Expression 1 =
`4x^(2)* x` =
`4x^(3)`

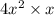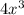
Expression 2 =
`(6x^(2))^(4)` =
`6x^(8)`

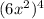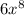
Now, the exponents in 1 is
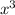`x^(3)` and in 2 is
`x^(8)`.

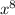Also,
`x^(8)>x^(3)`.

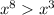Therefore, the exponents in expression 2 is greater than the exponents in expression 1.

Hence, option B i.e.'The exponents on Expression #2 are greater than the exponents of Expression #1' is correct.