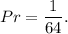Use the theoretical definition of probability
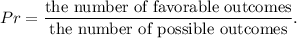
1. The number of all possible outcomes is
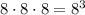 , because the first number can be selected from 8 numbers from the set {0, 1, 2, 3, 4, 5 ,6 ,7}, the second number can be selected from all 8 numbers from this set and the third number can be also selected from all 8 numbers from this set.
, because the first number can be selected from 8 numbers from the set {0, 1, 2, 3, 4, 5 ,6 ,7}, the second number can be selected from all 8 numbers from this set and the third number can be also selected from all 8 numbers from this set.
2. The number of favorable outcomes is 8. All favorable outcomes are:
- 0,0,0;
- 1,1,1;
- 2,2,2;
- 3,3,3;
- 4,4,4;
- 5,5,5;
- 6,6,6;
- 7,7,7.
3. The probability that the player will win a prize is
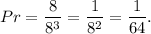
Answer: