Question

As a part of a contest, a computer picks a digit from 0 to 7, inclusive, 3 times. if the 3 digits are all the same, the contestant wins a prize. what is the probability that the player will win a prize?

Answer 1

There are 8 numbers for the computer to choose from.
So the probability of choosing a particular number is 1/8.
The first number can be any one of the 8.
The second and the third must be the same as the first, with probability 1/8.

Therefore the probability that all three numbers are the same
= (1/8)(1/8) = 1/64 [ player will win a prize ]
(=0.03125)

Answer 2

Use the theoretical definition of probability

`Pr=\frac{\text{the number of favorable outcomes}}{\text{the number of possible outcomes}}.`

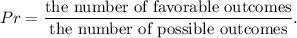
1. The number of all possible outcomes is
`8\cdot 8\cdot 8=8^3`, because the first number can be selected from 8 numbers from the set {0, 1, 2, 3, 4, 5 ,6 ,7}, the second number can be selected from all 8 numbers from this set and the third number can be also selected from all 8 numbers from this set.

2. The number of favorable outcomes is 8. All favorable outcomes are:

• 0,0,0;
• 1,1,1;
• 2,2,2;
• 3,3,3;
• 4,4,4;
• 5,5,5;
• 6,6,6;
• 7,7,7.

3. The probability that the player will win a prize is

`Pr=(8)/(8^3)=(1)/(8^2)=(1)/(64).`

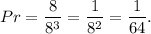
Answer:
`Pr=(1)/(64).`