Answer:
$19219.
Explanation:
We have been given that Alex purchased a new car for 28,000. The cars value depreciates 7.25% each year.
We will use exponential decay function to solve our given problem.
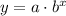 , where,
, where,
a = Initial value,
b = For decay b is in form (1-r), where r represents decay rate in decimal form.
Let us convert our given rate in decimal form.
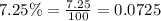
Upon substituting our given values in above formula we will get,
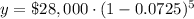
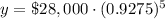

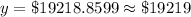
Therefore, the value of car 5 years after it is purchased will be $19219.