Question

Alex purchased a new car for 28,000. The cars value depreciates 7.25% each year. What will be value of the car 5 years after it is purchased? Round your answer to the newest dollar

Answer 1

If depreciation is 7.25% per year, then the common factor is (1-0.0725), or 0.9275.

Thus, the car's value after 5 years will be:

V = $28000(0.9275)^5 = $28000(0.6864) = $19218.86, or (to the nearest dollar) $19218 (answer)

Answer 2

$19219.

Explanation:

We have been given that Alex purchased a new car for 28,000. The cars value depreciates 7.25% each year.

We will use exponential decay function to solve our given problem.

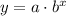`y=a\cdot b^x`, where,

a = Initial value,

b = For decay b is in form (1-r), where r represents decay rate in decimal form.

Let us convert our given rate in decimal form.

`7.25\%=(7.25)/(100)=0.0725`

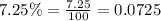
Upon substituting our given values in above formula we will get,

`y=\$28,000\cdot(1-0.0725)^5`

`y=\$28,000\cdot(0.9275)^5`

`y=\$28,000\cdot 0.686387856528418`

`y=\$19218.8599\approx \$19219`

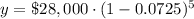
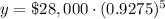
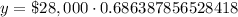
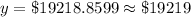
Therefore, the value of car 5 years after it is purchased will be $19219.