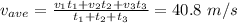Hello
Let's solve the problem in the three different steps
1) Uniformly accelerated motion, with acceleration
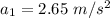
and for a total time of
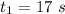
. The body is initially at rest, so the distance covered is given by
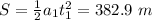
Calling

and
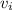
the final and initial velocity, and since the
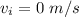
because the body starts from rest, we can use

to find the final velocity after this first leg:
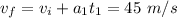
And the average velocity in this first leg is
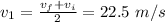
2) Uniform motion. The velocity is constant and it is equal to the final velocity of the first leg:
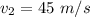
. This is also the average velocity of the second leg.
The total time of this second leg is
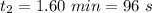
. The distance covered is given by
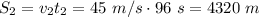
3) Uniformly decelerated motion, with constant deceleration of
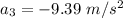
and for a total time of
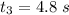
. Here, the initial velocity of the body is the final velocity of the previous leg, i.e.
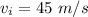
. Therefore, the distance covered in this leg is given by
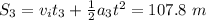
The final velocity in this leg is given by
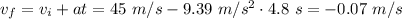
The negative sign means that after decelerating, the body has started to go in the opposite direction. Similarly to step 1, the average velocity in this leg is given by
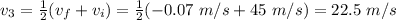
4) Finally, the total distance covered in the motion is
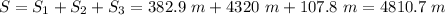
To find the average velocity, we must "weigh" the average velocity of each leg for the correspondent time of that leg: